熱文關注：

注冊測繪師考試復習需要哪些準備什么資料?需要多久?

漲知識：你知道常用的地球半徑差異符號表達式有哪些嗎？

地球半徑是測量和地球科學計算中最常用的基本參數，根據地球科學、空間科學、導航定位的要求和某些需求，常用到平均曲率半徑、平均球半徑、等距離球半徑、等面積球半徑和等體積球半徑這5種地球半徑。隨著空間技術和計算機技術在大地測量及地圖學中的應用和發展，研究常用地球半徑間的關系及它們之間的差異問題具有更加重要的實用價值。對于這一問題，國內外許多學者進行了研究，取得了顯著成果。文提出使用不同的球體半徑表示球體特性，將不同球體半徑代入克拉索夫斯基橢圓參數求得數值解，再代入球體面積公式，求得不同半徑下大圓航線長度和角度變形大小，發現使用等角球半徑計算大圓航線可以滿足航海使用精度要求。文獻將子午圈曲率半徑和卯酉圈曲率半徑展為大地緯度的冪級數，并且借助輔助函數V導出了不同形式的平均曲率半徑展開式。文獻中利用等距離球半徑和等面積球半徑，推導出常用緯度函數應用于求解地圖投影變換，提出了變系數線性插值方法，解決了測量和地圖學中所要求的計算精度問題。文獻利用球體半徑和計算機代數系統對大地測量學和地理信息系統中的問題進行了研究。

從目前來看，前人對這一領域作了很多卓有成效的工作，但主要是針對其中一種或幾種地球半徑進行計算和應用，多是對等角緯度、等面積緯度及等距離緯度的計算與分析[10-15]，很少有文獻將這幾種常用的地球半徑間的差異在符號和數值上進行系統的比較。計算機代數系統可以將基本的數學公式展開成冪級數形式，推導出的公式相對于人工計算具有更高的精確度。為豐富對這一問題的研究，使人們對這幾種常用地球半徑形成較直觀的認識，本文著重研究了常用地球半徑間的差異問題，推導出了常用地球半徑間差異符號表達式，最后以CGCS2000參考橢球[20]為例，對常用地球半徑間的差異進行了數值分析和比對，發現平均球半徑和等體積球半徑在等面積地圖投影中可以對等面積球半徑進行替換。

1 常用地球半徑定義

平均曲率半徑Ra常用于制作地球表面上局部地區地圖[21]，也可以取制圖區域中心點，記橢球偏心率為e，則它關于大地緯度B的表達式

就地球總體而言，平均球半徑(取地球橢球三軸半軸長的算術平均值，用于簡單決定球半徑)[22]、等面積球半徑(保持球體表面積等于地球橢球面相應全面積而決定的球半徑，主要用于等面積投影)[23]、等距離球半徑(使球面經線總長等于地球橢球面經線總長而決定的球半徑，主要用于等距離投影中)[24]和等體積球半徑(使地球球體的體積等于地球橢球體的體積來決定的球半徑)的表達式與大地緯度B無關，只取決于地球橢球模型的參數a、e，其表達式為

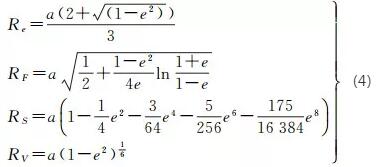
式中, Re表示平均球半徑;RF表示等面積球半徑;RS表示等距離球半徑;RV表示等體積半徑。

2 常用地球半徑間的差異符號表達式

由于5種常用地球半徑具有一定差異，在實際應用中會用到它們的差值表達式。為了解常用地球半徑間的差異情況，特別是差異最值點及其對應差異最值，可基于它們之間的差值表達式推導出其差異符號表達式。

2.1 平均曲率半徑與4種常用球體半徑間的差異符號表達式

通過對平均曲率半徑與4種常用球體半徑的表達式進行分析，即可推算出其差異符號表達式。以平均球半徑為例

。。。。

并以CGCS2000橢球為例對它們進行了數值分析和比對，得出如下結論。

(1) 平均曲率半徑與4種常用球體半徑差異值隨大地緯度的增大而增大，差異絕對值隨大地緯度的增大先減小后增大，在某一個特定點處差異值為0。其中，當B取

時，存在差異最大值，平均曲率半徑與等距離球半徑間差異最大，差異最大符號表達式的首項為

;B取0時，存在差異最小值，平均曲率半徑與平均球半徑間差異值最小，最小值符號表達式的首項為

。

(2) 平均曲率半徑是微觀上的平均值，是隨著大地緯度B逐點變化的;4種常用球體半徑是宏觀意義上的地球球體上的平均值，與大地緯度B無關。平均曲率半徑與4種常用球體半徑除在特殊點等價外，其余點無法進行相互代替應用。

(3) 4種常用球體半徑間，平均球半徑和等面積半徑間的差異絕對值最小，絕對值最小符號表達式的首項為

;平均球半徑和等距離半徑之間的差異絕對值最大，絕對值最大值符號表達式的首項為

。等距離球半徑與其余3種地球半徑差異較大，不能相互替代;平均球半徑和等體積球半徑與等面積球半徑之間差異較小，在實際應用過程中可以用平均球半徑和等體積球半徑來替代等面積球半徑。

(4) 將常用地球半徑間差異值表示為符號形式，并統一展開為偏心率e的冪級數形式，該表達式易于比較分析，一定程度上豐富了測量及地圖學數學分析理論。

注：以上內容來源于《測繪學報》《宗敬文:常用地球半徑差異符號表達式》一文，本文節選了部分內容。全文請查看原文獻。

根據《人力資源社會保障部辦公廳關于2019年度專業技術人員資格考試計劃及有關事項的通知》，2019年注冊測繪師考試時間是2019年9月7日—8日。

熱點關注：

點擊查看2019注冊測繪師報考條件>>

2019年注冊測繪師考試提分課程 

（責任編輯：gx）

共2頁,當前第1頁  第一頁  前一頁  下一頁